Question

Explain in words how you would graph the equation
`(1)/(3)x + y = 5`

Answer 1

The Slope-Intercept form of the equation of a line is:

`y=mx+b`

Where "m" is the slope of the line and "b" is the y-intercept.

You have the following equation:

`(1)/(3)x+y=5`

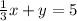
So you can solve for "y" in order to write it in Slope-Intercept form:

`y=-(1)/(3)x+5`

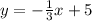
You can identify that:

`\begin{gathered} m=-(1)/(3) \\ \\ b=5 \end{gathered}`

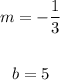
Knowing the slope and the y-intercept, you can graph the equation:

1. Plot the value of "b" on the Coordinate plane.

2. Remember that:

`m=(y_2-y_1)/(x_2-x_1)`

So the numerator indicates the number of units you need to move from the y-intercept and if you must move up or down, and the denominator indicates if you must move right or left and the number of units you need to move from the y-intercept.

In this case, since the slope is negative, you know that the line is decreasing from left to right, you must move 1 unit up and 3 units to the right. Then draw a second point.

3. The line will pass through the y-intercept and the second point found using the slope.

The answer is:

I would solve for "y" in order to write the equation in Slope-Intercept form. Then I would plot the y-intercept on the Coordinate plane to have the first point and use the slope to find the second point. Using the slope I'd move 1 unit up and 3 units to the right from the y-intercept. I'd draw the line passing through those points.