Question

1. Given R (7,-1), B(-3,-6), plot the points and trace the figure Part A a determine the lengths of each side (round to the nearest hundredth).prat B Determine the perimeter.

Answer 1

Given the points, we graph it as follows:

A. We determine the lengths of each side using the following expression:

`d=\sqrt[]{(X)^2+(Y)^2_{}}`

Here X & Y are the x & y-components from the directional vectors made from the points given.

Now, using the points we find the following directional directional vectors:

`RA=(3-7,-6+1)\Rightarrow RA=(-4,-5)`
`AB=(-3-3,-6+6)\Rightarrow AB=(-6,0)`
`BE=(-3+5,-6-4)\Rightarrow BE=(2,-10)`
`RE=(-5-7,4+1)\Rightarrow RE=(-12,5)`

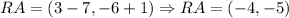
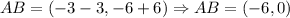
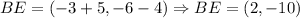
Now, we will determine the lengths of each side:

`d_(RA)=\sqrt[]{(-4)^2+(-5)^2}\Rightarrow d_(RA)=\sqrt[]{41}`
`d_(AB)=\sqrt[]{(-6)^2+(0)^2}\Rightarrow d_(AB)=6`
`d_(BE)=\sqrt[]{2^2+(-10)^2}\Rightarrow d_(BE)=2\sqrt[]{26}`
`d_(RE)=\sqrt[]{(-12)^2+5^2}\Rightarrow d_(RE)=13`

So, the lengths of each side are:

Side RA = 6.40 units.

Side AB = 6 units.

Side BE = 10.20 units.

Side RE = 13 units.

B. The approximate perimeter is:

6.40 + 6 + 10.20 + 13 = 55.4

So, its perimeter is approximately 55.4 units.