B
1) The best way to tackle this question is to think of the difference between two cubes:
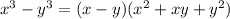
2) So now, let's apply to the binomial we have:
![\begin{gathered} \sqrt[3]{512}=8 \\ y^3-512=(y-8)(y^2+8y+64) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/qr2gdn11dohbnxtvmoz58x5grktdz6lz2r.png)
So now, let's make use of the factor zero property for the first factor and solve the quadratic using the quadratic formula:
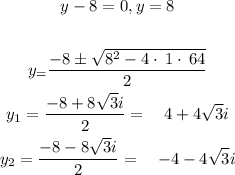
3) Thus, the answer is:
B