Question

Need help with #81, specifically don’t understand how to determine the domain

Answer 1

ANSWERS

a) Domain: x ∈ (-∞, -1) ∪ (-1, ∞)

b) Domain: x ∈ (-∞, 0) ∪ (0, ∞)

Step-by-step explanation

These compositions are:

a)

`f\circ g=f(g(x))=(2)/(g(x))=(2)/(x+1)`

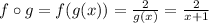
And

b)

`g\circ f=g(f(x))=f(x)+1=(2)/(x)+1`

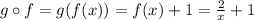
To find the domain in each function we have to find the values that x cannot take. If there aren't any, then the domain is all real values.

For composition a) note that x is in the denominator as (x+1). As we know, for real numbers the denominator can't be 0, so that's our restriction:

`x+1\\e0`

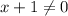
Solving for x:

`x\\e-1`

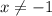
The domain for f º g is all real values except x = -1

For composition b) we have x in the denominator too, but it is alone. Therefore, as said before, x cannot be 0.