Question

What is the speed of the airplane in still air?(Remember, x = speed of airplane in still air.)Here's our system of equations:2(x + y) = 6003(x - y) = 600Enter the correct answer.2OOOODONENow we can solve the problem.LOClear all2ProblemAt full speed, Hal travels 600 miles in 2 hourswith the wind. The same distance againstthe wind takes 3 hours.What's the maximum speed of Hal's airplanein still air? What's the speed of the wind?x = speed of the airplane in still airy = speed of the wind

Answer 1

Well, from the statement of the problem we have the following equations:

`\begin{gathered} 2\cdot(x+y)=600 \\ 3\cdot(x-y)=600 \end{gathered}`

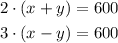
And they ask us about the value of the variable: x = speed of the airplane in still air

So, we only need to solve system of equations in order to find the answer.

There are many ways to solve this system of equations. One way is the following.

We rewrite the equations:

`\begin{gathered} 2x+2y=600 \\ 3x-3y=600 \end{gathered}`

Then we multiply the first equation by 3 and the second equation by 2:

`\begin{gathered} 6x+6y=1800 \\ 6x-6y=1200 \end{gathered}`

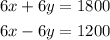
(the multiplication is made multiplying each term)

Now we can add the two equations:

`\begin{gathered} (6x+6y)+(6x-6y)=1800+1200 \\ 12x=3000 \end{gathered}`

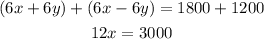
And from the last equation we find that:

`x=250`

The answer is: x = speed of the airplane in still air = 250