From the figure, we have the coordinates of ABC:'
A(-5, 1), B(-3, 4), C(0, 1)
Given the rule of the translations:
(x, y) ==> (x + 3, y + 2)
Translation is a form of rigid transformation which just moves the figure. Translation only changes the position of a figure but it does not change the shape of the size of the figure.
Using the translation rule, we have the coordinates of A'B'C':
A'(-5+3, 1+2) ==> A'(-2, 3)
B'(-3+3, 4+2) ==> B'(0, 6)
C'(0+3, 1+2) ==> C'(3, 3)
The coordinates are:
A'(-2, 3), B'(0, 6), C'(3, 3)
This means the triangle ABC moved 3 units up and 2 units to the right.
Let's answer the following:
• (a). If the slope of BC is -1, let's determine the slope of B'C'.
Since translation does not change the shape nor the size, the slope of B'C' will also be -1.
• (b). ,If the length of BC is 3√2, the length of B'C' will also be 3√2. This is because translation does not change the size of an object.
• (c). ,Determine the length of AC and A'C'
Apply the distance formula:
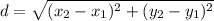
• Length of AC:
Where:
(x1, y1) ==> A(-5, 1)
(x2, y2) ==> B(0, 1)
Thus, we have:
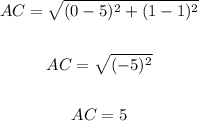
The length of AC is 5.
• Length of A'C'
Where:
(x1, y1) ==> A'(-2, 3)
(x2, y2) ==> C'(3, 3)
We have:
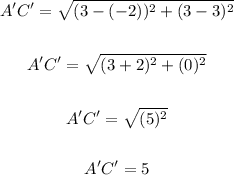
The length of A'C' is also 5 units.
• (d). Slope of AC and A'C'
AC and A'C' are horizontal lines.
The slope of any horizontal line is always zero.
Therefore the slope of AC and A'C' are 0.
ANSWER:
• (a) Slope of B'C' = -1
,
• (b). Length of B'C' = 3√2
,
• (c). Length of AC = 5
Length of A'C' = 5
• (d). Slope of AC = 0
Slope of A'C' = 0