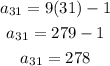Question

The first three terms of a sequence are given. Round to the nearest thousandth (if necessary). 8, 17, 26, ... Find the 31st term.

Answer 1

Start by identifying if the sequence is geometric or arithmetic.

since there is a common difference between the numbers the sequence is arithmetic

Find the common difference

`\begin{gathered} 26-17=9 \\ 17-8=9 \end{gathered}`

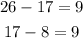
The common difference is 9.

Use the formula for arithmetic sequence

`a_n=a_1+(n-1)\cdot d`

in which

a1= first term

d= common difference

n= position

rewrite with the information given

`a_n=8+(n-1)\cdot9`

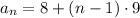
simplify

`\begin{gathered} a_n=8+9n-9 \\ a_n=9n-1 \end{gathered}`

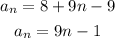
replace n by 31 to find the 31st term

`\begin{gathered} a_(31)=9(31)-1 \\ a_(31)=279-1 \\ a_(31)=278 \end{gathered}`