To solve this problem, we could use the following model
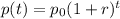
Where p0 represents our population in millions, r represents the growth rate, and t represents the amount of years after 2011( 2011 is t = 0).
We have all of our values
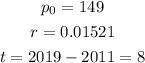
Plugging those values in our model, we have
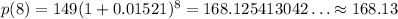
Then, the size of the population in 2019 will be about 168.13 million.