Question

You are planning to rent a car for a road trip. Company A charges a base price of $56 plus a charge of 0.25 per mile. A competing car company, Company B, charges a base price of $45 plus a charge of $0.58 per mile,(a) Write a formula for the total cost Ca, of renting a car from Company A as a function of the number of miles, m: driven.(b) Write a formula for the total cost Cb , of renting a car from Company B as a function of the number of miles, m. driven.(c) At what mileage will the cost of renting a car be the same from both companies? Round decimal to two places.

Answer 1

Part a)

Since m is the number of miles driven and company A charges a base price of $56 plus a charge of $0.25 per mile, we can write the following equation:

`Ca=56+0.25m`

Part b)

Again, since m is the number of miles driven and company B charges a base price of $45 plus a charge of $0.58 per mile, we can write the following equation:

`Cb=45+0.58m`

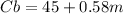
Part c)

The cost of renting a car from both companies will be the same when:

`Ca=Cb`

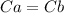
Then, we solve the following equation for m:

`\begin{gathered} 56+0.25m=45+0.58m \\ \text{ Subtract 56 from both sides of the equation} \\ 56+0.25m-56=45+0.58m-56 \\ 0.25m=0.58m-10 \\ \text{ Subtract 0.58 m from both sides of the equation} \\ 0.25m-0.58m=0.58m-10-0.58m \\ -0.33m=-10 \\ \text{ Divide by 0.33 from both sides of the equation} \\ (-0.33m)/(-0.33)=(-10)/(-0.33) \\ m\approx33.33\Rightarrow\text{ The symbol }\approx\text{ is read`

Therefore, the cost of renting a car from both companies will be the same at 33.33 miles.