Question

Some of the first n terms of the geometric sequence

Answer 1

1) We have to find the sum of the first four terms of the geometric sequence:

`3+3((1)/(4))+3((1)/(4))^2+3((1)/(3))^3+3((1)/(4))^4`

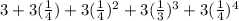
In this case, we can take out the factor 3 and we have a common ratio r = 1/4. We have to add the first 5 terms.

Then, the sum can be expressed as:

`S_n=(a_1(1-r^n))/(1-r)`

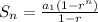
For this problem, r1 = 3, r = 1/4 and n = 5:

`\begin{gathered} S_5=(3(1-((1)/(4))^5))/(1-(1)/(4)) \\ S_5=(3(1-(1)/(1024)_))/((3)/(4)) \\ S_5=(3((1024-1)/(1024)))/((3)/(4)) \\ S_5=(4)/(3)\cdot3\cdot(1023)/(1024) \\ S_5=(1023)/(256) \end{gathered}`

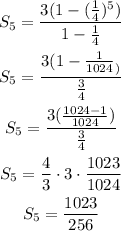
2) We have this sum already solved but we can check it as:

`\begin{gathered} S=\sum_{i\mathop{=}1}^7(-3)^i \\ S=(-3)+(-3)^2+(-3)^3+(-3)^4+(-3)^5+(-3)^6+(-3)^7 \\ S=-3+9-27+81-243+729-2187 \\ S=-1641 \end{gathered}`

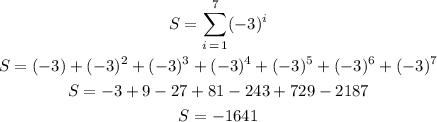
Answer:

1) 1023/256

2) -1641