hello, to solve this question, we need to look the function:
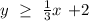
So, let's see the graphics:
remember: for this question, only values equal to or greater than y are of interest
We can solve by attempts:
when x = 0:
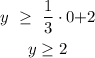
At this moment, we can discard two options: A and C.
Why? Because when x = 0, just interest for us y>= 2.
when x = 1:
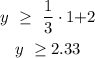
when x = 2:
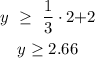
As we have the sign "greater than or equal to", we can conclude that it is a closed representation, so the line must be continuous.
Right answer: B.