Question

span. The following ordered pairs shows the population and the year over the ten-year span, (population, year) for specific recorded years:(2500,2000),(2650,2001),(3000,2003),(3500,2006),(4200,2010)Using this tool we find the linear regression line to be y=Answer Type your answer without spaces or commas and rounded to the nearest hundredth.The population will hit 8,000 in the year Answer Using this tool we find the r-value to be Answer

Answer 1

Given the ordered pairs:

(2500, 2000), (2650, 2001), (3000, 2003), (3500, 2006), (4200, 2010)

Let's find the linear regression line.

Apply the formula:

y = mx + b

Where m si the slope and b is the y-intercept.

To find the slope, apply the formula:

`m=\frac{n(\sum^{}_{}xy)-\sum^{}_{}x\sum^{}_{}y}{n(\sum^{}_{}x^2)-(\sum^{}_{}x)^2}`

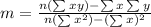
Where:

∑x = 2500 + 2650 + 3000 + 3500 + 4200 = 15850

∑y = 2000 + 2001 + 2003 + 2006 + 2010 = 10020

∑xy = (2500 * 2000) + (2650 * 2001) + (3000 * 2003) + (3500 * 2006) +(4200 * 2010) = 31774650

∑x² = 2500² + 2650² + 3000² + 3500² + 4200² = 52162500

∑y² = 2000² + 2001² + 2003² + 2006² + 2010² = 20080146

n = number of ordered pairs = 5

Thus, we have:

`\begin{gathered} m=(5(31774650)-15850\ast10020)/(5(52162500)-(15850)^2) \\ \\ m=0.00587 \end{gathered}`

The slope of the regression line is 0.00587

To find the y-intercept, apply the formula:

`b=\frac{(\sum ^{}_{}y)(\sum ^{}_{}x^2)-\sum ^{}_{}x\sum ^{}_{}xy}{n(\sum ^{}_{}x^2)-(\sum ^{}_{}x)^2}`

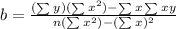
Thus, we have:

`\begin{gathered} b=((10020)(52162500)-15850\ast10020)/(5(52162500)-(15850)^2) \\ \\ b=1985.41 \end{gathered}`

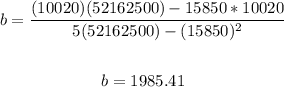
Therefore, the regression line is:

`y=0.00587x+1985.41`

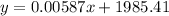
To determine the year the population will hit 8000, substitute 8000 for x and solve for y:

`\begin{gathered} y=0.00587(8000)+1985.41 \\ \\ y=46.92+1985.41 \\ \\ x=2032.33 \end{gathered}`

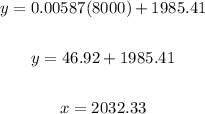
Therefore, the population will hit 8000 in the year 2032.

To find the R-value, apply the formula:

`R=\frac{n(\sum ^{}_{}xy)-\sum ^{}_{}x\sum ^{}_{}y}{(n(\sum ^{}_{}x^2)-(\sum ^{}_{}x)^2)-(n(\sum ^{}_{}y^2^{})-(\sum ^{}_{}y)^2}`

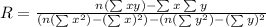
Thus, we have:

`\begin{gathered} R=(5(31774650)-15850\ast10020)/(√(5(52162500)-(15850)^2)-(5(20080146)-(10020)^2)) \\ \\ R=18.16 \end{gathered}`

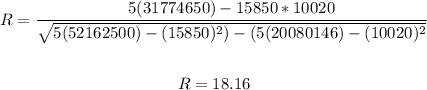
The R value is