Question

There is a population of 9,000 bacteria in a colony. If the number of bacteria doubles every 245 hours, what will the population be 980 hours from now?

Answer 1

There is a population of 9,000 bacteria in a colony.

If the number of bacteria doubles every 245 hours, what will the population be 980 hours from now?

Recall that the exponential growth formula is given by

`y=a\cdot b^x`

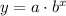
Where a is the initial population, b is the rate of growth, and x is the time.

For the given case, we have

a = 9,000

b = 2 (doubles)

x = 980/245 = 4

Let us substitute these values into the above formula

`\begin{gathered} y=a\cdot b^x \\ y=9,000\cdot2^4 \\ y=9,000\cdot16 \\ y=144,000 \end{gathered}`

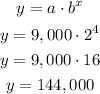
Therefore, the population of the bacteria will be 144,000 after 980 hours from now.