Question

Use the discriminant to determine whether the function has complex zeros.

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given function

`f(x)=2x^2-x+1`

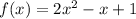
STEP 2: Write the formula for calculating the discriminant

`\begin{gathered} Given\text{ a standard form of quadratic equation below:} \\ f(x)=ax^2+bx+c \\ The\text{ discriminant is given as:} \\ b^2-4ac \end{gathered}`

STEP 3: Calculate the discriminant of the given function

`\begin{gathered} \text{For the given function,} \\ a=2,b=-1,c=1 \\ discriminant=b^2-4ac \\ discriminant=(-1)^2-4(2)(1)=1-8=-7 \end{gathered}`

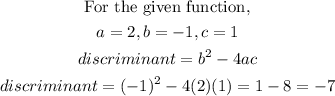
Discriminant = -7

STEP 4: Write the conditions for using the discriminant to determine the roots(zeros) of a quadratic function.

If the discriminant of the function is greater than zero, then the function has two real roots

If the discriminant of the function is less than zero, then the function has imaginary or complex roots

If the discriminant of the function is equal to zero, then the function has one real root

Since the discriminant is -7 which is less than zero, hence, the function has complex roots