We have the following triangle
We have the hypotenuse and all the angles so we can use the law of sines
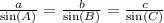
In this case take us a = 4, b = QP andc = RQ
First, we solve QP
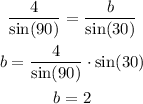
Second. we solve RQ
![\begin{gathered} (4)/(\sin(90))=(c)/(\sin(60)) \\ c=(4)/(\sin(90))\cdot\sin (60) \\ c=2\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/4omjjcy5pn2inalenxjlilbzo67wpiuap2.png)
These are the solutions
To check this we can take out the hypotenuse using the Pythagoras theorem and check that
![\begin{gathered} H=\sqrt[]{(2)^2+(2\sqrt[]{3})^2} \\ H=\sqrt[]{4+(4\cdot3)} \\ H=\sqrt[]{4+12} \\ H=\sqrt[]{16} \\ H=4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/iw87k4yzr5n2vz9yoger7ir384fyuq5p8w.png)
This is correct
In conclusion, these answers are:
![\begin{gathered} QP=2 \\ RQ=2\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/x8vpn6ldytcu1tndf3vn83x1m3kcvm2ku3.png)