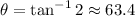Question

a +80 microcoulombs point charge placed at the origin. calculate magnitude and direction of the Electric Field created by this point charge at the following locations a) at point p (5m, 0) and b) at point S (2m, 4m)

Answer 1

ANSWERS

(a) E = 28800 N/C, direction 0°

(b) E = 36000 N/C, direction 63.4°

Step-by-step explanation

Given:

• The charge, q = +80 μC

,

• The location of the charge q, (0, 0)

,

• The coordinates of points P(5m, 0) and S(2m, 4m)

Find:

• The magnitude and direction of the electric field, E, at points P and S

The magnitude of the electric field created by a charge q at a distance r from the charge is,

`E=k(q)/(r^2)`

Where k is Coulomb's constant and has an approximate value of 9x10⁹ Nm²/C².

(a) We have to find the distance from the charge to point P,

Both the charge and the point are on the x-axis, so the distance is the horizontal distance between them: 5m.

The magnitude of the electric field is,

`E=k\cdot(q)/(r^2)=9\cdot10^9(Nm^2)/(C^2)\cdot(80\cdot10^(-6)C)/(5^2m^2)=28800(N)/(C)`

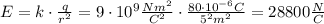
Positive charges create fields that point radially away from them. Since q is a positive charge, the direction of its electric field at point P is in the positive x-direction, which is 0 degrees.

(b) For point S we will have to use the Pythagorean theorem to find the distance to the charge,

With the diagram above we will find the distance from point S to the charge and the direction of the electric field, θ.

The distance squared is,

`r^2=2^2+4^2=4+16=20`

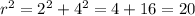
So the magnitude of the electric field is,

`E=k\cdot(q)/(r^2)=9\cdot10^9(Nm^2)/(C^2)\cdot(80\cdot10^(-6)C)/(20m^2)=36000(N)/(C)`

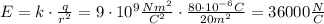
As explained in part a, positive charges create electric fields pointing radially away from them, so the direction of this electric field is given by the angle θ,

`\tan\theta=(4m)/(2m)`

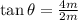
Solving for θ,

`\theta=\tan^(-1)2\approx63.4\degree`