There are:
36 heads and 102 feet.
The total number of animals (pigs+geese) are 36, also we know that the pigs have 4 feet and the geese 2.
Therefore, the equations to find it will be:
1. For the heads:
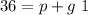
For the feet:
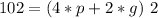
Where p=pigs and g= geese.
Solving the equations using substitution method:
Isolating p in (1):

Substituing (3) in (2):

Solving for g:
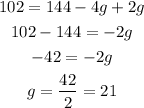
Finally, putting g=21 in (3):
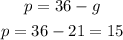
Answer: There are 15 pigs and 21 geese.