We have to find the orthocenter of the triangle FGI.
We start by graphing the vertices F, G and I:
The next step is to calculate the slope of each segment, then its perpendicular line that pass through the other vertex of the triangle (not included in the segment).
With two segments is enough to calculate the orthocenter.
Segment GI.
Slope:
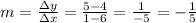
Perpendicular slope:
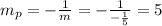
Line equation (perpendicular) that pass through F(3,1):
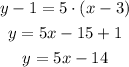
Segment GF.
Slope:
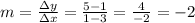
Perpendicular slope:
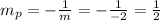
Line equation (perpendicular) that pass through I(6,4):
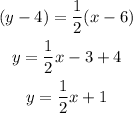
Then, with two lines, we can find the intersection:
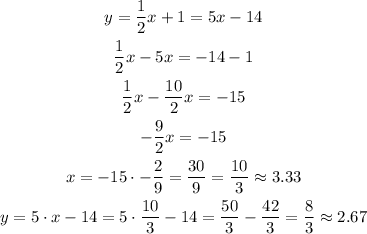
The orthocenter is (x,y) = (10/3, 8/3) = (3.33, 2.67)