Question

Use the graph to find when f(x)

Answer 1

Answer:

x > -7

Explanations:

For the graph g(x), select two points on the line

(-7, 4) and (-2, 8)

That is, x₁ = -7, y₁ = 4, x₂ = -2, y₂ = 8

The slope of the line is given as:

`\begin{gathered} m\text{ = }(y_2-y_1)/(x_2-x_1) \\ m\text{ = }(8-4)/(-2-(-7)) \\ m\text{ = }(4)/(5) \end{gathered}`

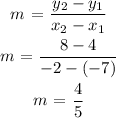
The equation of a line is given as:

`\begin{gathered} y-y_1=m(x-x_1) \\ y\text{ - 4 = }(4)/(5)(x-(-7)) \\ y\text{ - 4 = }(4)/(5)(x+7) \\ y-4=(4)/(5)x+(28)/(5) \\ y\text{ = }(4)/(5)x+(28)/(5)+4 \\ y\text{ = }(4)/(5)x\text{ + }(48)/(5) \\ y\text{ = }0.8x+9.6 \\ g(x)\text{ = 0.8x+9.6} \end{gathered}`

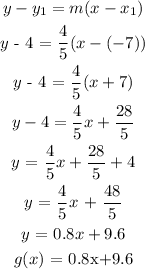
For the graph f(x):

Select the points (-7, 4) and (-3, 2)

`\begin{gathered} m\text{ = }(2-4)/(-3-(-7)) \\ m\text{ = }(-2)/(4) \\ m\text{ = -0.5} \end{gathered}`

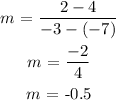
The equation of the line is:

`\begin{gathered} y-y_1=m(x-x_1) \\ y\text{ - 4 = -0.5(x - (-7)} \\ y\text{ - 4 = -0.5(x + 7)} \\ y\text{ - 4 = -0.5x - }3.5 \\ y\text{ = -0.5x - 3.5 + 4} \\ y\text{ = -0.5x + 0.5} \\ f(x)\text{ = -0.5x + 0.5} \end{gathered}`

f(x) < g(x)

-0.5x + 0.5 < 0.8x + 9.6

-0.5x - 0.8x < 9.6 - 0.5

-1.3x < 9.1

-x < 9.1 / 1.3

-x < 7

x > -7