When a line bisect an angle this means that it divide the total angle in two equal angles.
Then we can conclude than
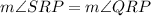
But we know that
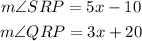
Then, plugging this in the first equation
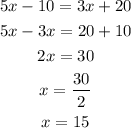
Once we have the value of x we can determine the value of the angles SRP and QRP
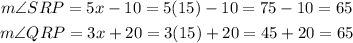
Finally, to find the angle SRQ, we only add both angles. Then
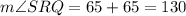
So the angle SRQ is 130 degrees.