Question

In the diagram, RP bisects SRQ. if SRP =5x-10 and QRP=3x+20, what is the measure in degrees of SQR

Answer 1

When a line bisect an angle this means that it divide the total angle in two equal angles.

Then we can conclude than

`m\angle SRP=m\angle QRP`

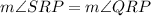
But we know that

`\begin{gathered} m\angle SRP=5x-10 \\ m\angle QRP=3x+20 \end{gathered}`

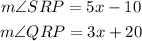
Then, plugging this in the first equation

`\begin{gathered} 5x-10=3x+20 \\ 5x-3x=20+10 \\ 2x=30 \\ x=(30)/(2) \\ x=15 \end{gathered}`

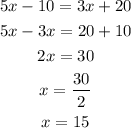
Once we have the value of x we can determine the value of the angles SRP and QRP

`\begin{gathered} m\angle SRP=5x-10=5(15)-10=75-10=65 \\ m\angle QRP=3x+20=3(15)+20=45+20=65 \end{gathered}`

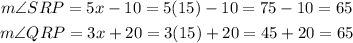
Finally, to find the angle SRQ, we only add both angles. Then

`m\angle SRQ=65+65=130`

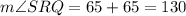
So the angle SRQ is 130 degrees.