C(2.5,-1)
Step-by-step explanation
Step 1
if the points A and B are the endpoints of the diameter, we can find the midpoint to find the coordiantes of the center, the midpoint of P1 and P2 is given by:
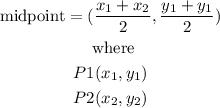
Let
P1=A(8,-4) P2=(-3,2)
midpoint C
Step 2
replace
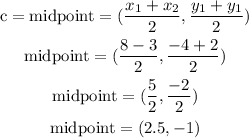
so, the answer is C(2.5,-1)