To find the domain of a function, look for the restrictions over the functions involved in it.
![\text{Let }f(x)=\log _3(\sqrt[]{x}+1)](https://img.qammunity.org/2023/formulas/mathematics/college/rhqpjmyxkfti6oovqeqjdcqo9xgpjphuxs.png)
The log functions are defined whenever their argument is greater than 0. This means:
![\sqrt[]{x}+1>0](https://img.qammunity.org/2023/formulas/mathematics/college/bafm31ipmxrqd307kynfdmkdiiu3s5hvc8.png)
Since 1>0 and the square root of x is always greater than or equal to 0, then this does not restrict the domain of the function.
Nevertheless, the square root of x requires that:
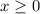
This is the only restriction over the variable x.
Therefore, the domain of the function, is:

Next, solve the equation:
![\log _3(\sqrt[]{x}+1)=1](https://img.qammunity.org/2023/formulas/mathematics/college/618km3t13s1if2694szgxcyt9518224drq.png)
Notice that given this equation, then 3 to the power of each side of the equation should be equal:
![3^{\log _3(\sqrt[]{x}+1)}=3^1](https://img.qammunity.org/2023/formulas/mathematics/college/p1wdlf8fh3zsyzwhnok0oi7r2qo87ougry.png)
Use the fact that:
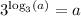
to simplify the equation:
![\begin{gathered} 3^{\log _3(\sqrt[]{x}+1)}=3^1 \\ \Rightarrow \\ \sqrt[]{x}+1=3^1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/is4n6or0l3rwfbeveiz8s6cm3ikq0z8x3m.png)
Simplify the power 3^1:
![\sqrt[]{x}+1=3](https://img.qammunity.org/2023/formulas/mathematics/college/wkp901dxgbtuownsnvgg5868z13hhdivr9.png)
Substract 1 from both sides of the equation:
![\sqrt[]{x}=2](https://img.qammunity.org/2023/formulas/mathematics/college/lkz7glhvvkshlkx0y8e70469j8h1gzm1f8.png)
Square both sides of the equation:
![(\sqrt[]{x})^2=2^2](https://img.qammunity.org/2023/formulas/mathematics/college/9ehdkpl3mllq3r8kw638sjivg0gewpx4ro.png)
Simplify the powers:

Check the answer by plugging in x=4 into the equation:
![\begin{gathered} \log _3(\sqrt[]{x}+1)=1 \\ \Rightarrow \\ \log _3(\sqrt[]{4}+1)=1 \\ \Rightarrow \\ \log _3(2+1)=1 \\ \Rightarrow \\ \log _3(3)=1 \\ \Rightarrow \\ 1=1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/7zf4byo7ducjf1k7njo8mumciummsorvfy.png)
Since we got an identity, the answer x=4 is correct.