Question

A beam of white light is incident on a prism at an angle of incidence of 71.2 degrees. The speed of red light in the prism material is 1.984 x 10^8 meters per second, and the speed of violet light in the prism material is 1.951 x 10^8 meters per second.a. At what angle does the red light enter the prism?b. At what angle does the violet light enter the prism?

Answer 1

`\begin{gathered} (a)\text{ }38.8\degree \\ (b)\text{ }38\degree \end{gathered}`

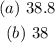
Step-by-step explanation

Parameters given:

Incident angle of white light, θ1 = 71.2 degrees

Speed of red light in the prism, vr = 1.984 * 10^8 m/s

Speed of violet light in the prism, vv = 1.951 * 10^8 m/s

Speed of light in air, v = 3 * 10^8 m/s

(a) To find the angle at which the red light enters the prism, apply the relationship given by Snell's law:

`{(v)/(v_r)}=(\sin\theta_1)/(\sin\theta_r)`

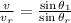
where v = speed of light in air

vr = speed of red light in the prism

θr = angle of refraction (angle that the light enters the prism)

Hence, solving for θr, we have that the angle at which the red light enters the prism is:

`\begin{gathered} (3*10^8)/(1.984*10^8)=(\sin71.2)/(\sin\theta_r) \\ \\ \sin\theta_r=(1.984*\sin71.2)/(3)=0.6261 \\ \\ \theta_r=\sin^(-1)(0.6261) \\ \theta_r=38.8\degree \end{gathered}`

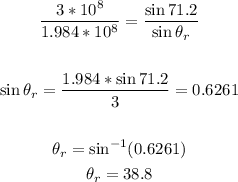
That is the answer.

(b)To find the angle at which the violet light enters the prism, apply the same formula above for violet light:

`(v)/(v_v)=(\sin\theta_1)/(\sin\theta_v)`

Hence, solving for θv, we have that the angle at which the violet light enters the prism is:

`\begin{gathered} (3*10^8)/(1.951*10^8)=(\sin71.2)/(\sin\theta_v) \\ \\ \sin\theta_v=(1.951*\sin71.2)/(3)=0.6156 \\ \\ \theta_v=\sin^(-1)(0.6156) \\ \theta_v=38\degree \end{gathered}`

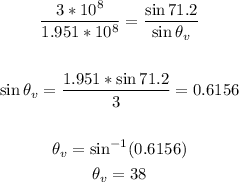
That is the answer.