Question

What is the sum of the geometric series in which a1 = 2, r = 3, and an = 486?

Answer 1

In order to determine the sum of the geometric series, proceed as follow:

Use the following expression for an:

`a_n=a_1r^(n-1)`

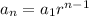
where,

a1 = 2

r = 3

an = 486

Replace the previous values into the expression for an, solve for n and simplify:

`\begin{gathered} 486=2\cdot3^(n-1) \\ (486)/(2)=3^(n-1) \\ 243=3^(n-1) \\ 3^5=3^(n-1) \end{gathered}`

Then, it is necessary that n = 6, because n - 1 = 6 - 1 = 5 and the previous equation is consistent.

Now, consider that the sum of the geometric series is given by:

`S_n=a_1((1-r^n)/(1-r))`

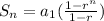
Replace the values of the parameters and simplify:

`S_6=2((1-3^6)/(1-3))=2((1-729)/(-2))=728`

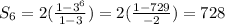
Hence, the result is 728