Question

You take a picture of a painting at an art gallery. The painting is above eye level, and you frame the painting so the top and bottom match with the top and bottom of your view ſindur. Your camera's auto-focus feature focuses at the height of the angle bisector shown in the diagram. How far from the bottom of the painting is the focus? 92 in. 52 in. Camera's line of focus 68 in.

Answer 1

Let us first find the complete angle that the camera is making

Recall from the trigonometric ratios

`\tan \theta=\frac{\text{opposite}}{\text{adjacent}}`

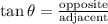
From the figure, we see that the opposite is 52 in and adjacent is 68 in

`\begin{gathered} \tan \theta=(52)/(68) \\ \theta=\tan ^(-1)((52)/(68)) \\ \theta=37.405\degree \end{gathered}`

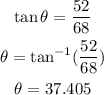
Since the camera's line of focus is the angle bisector then

`\theta=(37.405\degree)/(2)=18.7\degree`

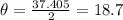
So, again using the trigonometric ratio, we can find x

`\begin{gathered} \tan \theta=\frac{\text{opposite}}{\text{adjacent}} \\ \tan (18.7)=(x)/(68) \\ x=\tan (18.7)\cdot68 \\ x=0.338\cdot68 \\ x=23.017\: in \end{gathered}`

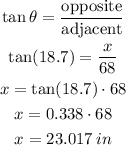
Therefore, the value of x is 23.017 inches.