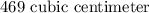1 Answer

Yogev · Answer 1 · 2023-07-20T14:29:42+0000

Answer:

The volume of the new cone would be;

$469\text{ cubic centimeter}$

Step-by-step explanation:

Given the cone in the attached image.

with radius r and height h of;

$\begin{gathered} r=4\operatorname{cm} \\ h=5\operatorname{cm} \end{gathered}$

If the radius was doubled and the height changed to 7cm, we would have;

$\begin{gathered} r_1=2(4\operatorname{cm})=8\operatorname{cm} \\ h_1=7\operatorname{cm} \end{gathered}$

The Volume of a cone can be calculated using the formula;

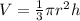
$V=(1)/(3)\pi r^2h$

substituting the new radius and height;

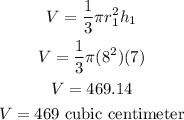
$\begin{gathered} V=(1)/(3)\pi r^2_1h_1 \\ V=(1)/(3)\pi(8^2)(7) \\ V=469.14 \\ V=469\text{ cubic centimeter} \end{gathered}$

Therefore, the volume of the new cone would be;

$469\text{ cubic centimeter}$

Please log in or register to add a comment.