The probability of the stick's weight being 1.87 oz or greater is 0.68%
STEP - BY - STEP EXPLANATION
What to find?
Probability of the stick's weight being 1.87 oz or greater.
Given:
• Mean μ = 1.50
,
• Standard deviation σ = 0.15
To solve the problem given, we will follow the steps below:
Step 1
State the formula needed to solve the problem given.
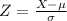
Step 2
State the required probability.
The reqyuired probability is;
P(X ≥ 1. 87) = 1 - P(X < 1.87)
Step 3
Substitute the values into the formula and simplify.
That is;
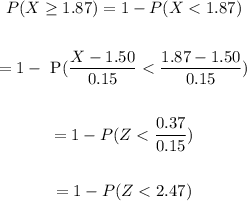
Step 4
Use the Z- distribution table to determine the value of P(Z<2.47).
Using z distribution table, looking 2.0 in the left column and 0.47 in the top most row, then selecting the intersecting cell, we get 0.9932.
Step 5
Substitute the value of P(Z<2.47) into:
P(X ≥ 1. 87) = 1 - P(Z<2.47))
= 1 - 0.9932
=0.0068
Step 6
Convert the result in step 5 to percentage by multiplying by 100.
P(X ≥ 1. 87) =0.0068 * 100 =0.68 %
Thereore, the probability of the stick's weight being 1.87 oz or greater is 0.68%