Question

Mathematical formulas model phenomena in every facet of our lives. Provide an example of how equations solve problems in a variety of situations.

Answer 1

In real-world terms, an equation can be defined by a process of making a situation equal to another situation.

Situations are defined by one or more variables, these variables are elements of an equation.

Mathematically an equation looks like this:

`x+y=5`

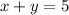
x and y are variables which if the appropriate values is used to replace them will satisfy the statement x + y =5, When x=2, y would be 3, when x =1 ,y =4 and when x=5, y is nothing. This illustration gives an insight on what a real-world situation could be like.

Take, for instance, the area of economy, the demand of commodity could influence the supply of such commodity provided there is an infinite number in the commodity produced, as the demand of the commodity increases, there would be a need for more supply of such commodity to satisfy customers need. This situation could be explained better under an area of mathematics called variation. Thus, if the relationship between the demand of a commodity and the supply is direct, this can be expressed mathematically as

`\begin{gathered} \text{If }D\text{ represent the demand} \\ S\text{ represent the supply} \\ \text{Then,} \\ D\propto S \end{gathered}`

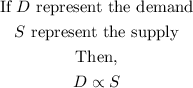
This can be written with the equal sign by introducing a constant of proportionality, If it is assumed that the price does not change, then

`D=PS\text{ (where P is price and it is constant.)}`

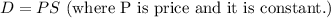
For every value of D, and at a particular price, the value of S can be obtained and vise versa

Hence, the above explanation is an example of how an equation solves the problems in one of variety of situations