STEP - BY - STEP EXPLANATION
What to do?
Compute a 99% confidence interval for the proportion of customers who have experienced a service interruption during the previous month.
Given:
X = 75
number of internet service provider ( n ) = 540
Here , X be a customers that experienced an interruption in high speed service during the previous month
X = 75.
And number of internet service provider ( n ) = 540
Proportion of interruption in high-speed provider in previous month is
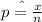
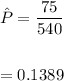
Formula of one sample proportion is :
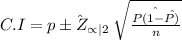
where;
zα/2= 2.58 (standard normal table value for Z0.005 )
Now;
Substitute the values into the formula.

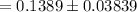
Confidence interval= (0.101, 0.177)
Hence, 99% confidence interval for proportion of customer who have experienced a service interruption during the previous month is ( 0.101 , 0.177)