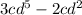The given expression is-
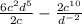
We can solve this using the cross method to subtract the fractions. The following property shows this method.
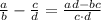
Using this property, we have
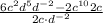
Now, we solve the products.
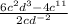
We simplify the terms since all of them can be divide by 2c
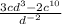
At last, we use the negative exponent property. This property allows us to change the position of the power with negative exponent.
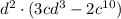
At last, we solve this product using the distributive property.
Therefore, the equivalent expression is