Question

Please help me with this

Answer 1

First make the graph

these triangles have similar shapes, could be congruent

then we can use a law to simplify because the angle TQP and RQS are congruents too, because these are opposite by the vertex

if two angles of each triangle are congruents or equals the third will be congruent with the other

now we know the triangles have the same angles but the measures of the side are diferent but proportional to other triangle with the same angles

then on this case we will arrange the triangles to see which sides are equivalent

the siodes will be equivalents and proportional, for example the side of the left triange 4mi is proportional to the right triangle with 8mi, how we find the proportional ratio?

we divide the value of the triangle where I want to find an unknow between the value of the other triangle

`(4)/(8)=(1)/(2)`

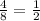
the if we multiply the ratio but any side of the rignt triangle we will obtain the value of the side on left triang

If we divide the length of any side of the left triangle between the ratio we obtain the value of the other triangle

then to find m we multiply the equavalent side by the ratio

`\begin{gathered} m=10*(1)/(2) \\ \\ m=5 \end{gathered}`

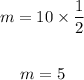
the value of 5 is 5 miles

if you want practice can find the equivalnte side to 3mi dividing the side between the ratio

`(3)/((1)/(2))=(3*2)/(1)=6`

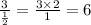
side X is 6mi