We want to know what value of width will maximize the area of the pigs. This is, we want to find a maximum of the function:
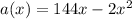
For doing so, we will find its critical points, by the first derivative criteria. Then we find the first derivative:
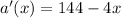
We equal to zero and solve for x:
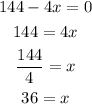
This means that x=36 is a critical point. Now, we will check if it is a maximum or a minimum using the second derivative test:

As the second derivative is negative for all x, this means that x=36 is a maximum of the funtion a(x).
On other words, the farmer should use a width of 36 feet to have the maximum area for his pigs.