This problem describes a situation where a college buys 2500 tennis balls for $0.50 each plus a fee of $800 for the logo. They then sell the balls for $2.50 each. We need to determine the average cost of each tennis ball and the profit the college will have if they manage to sell all the balls at that price.
To find the average cost, we need to add the price they paid per ball plus the one-time fee, then divide by the number of balls. We have:
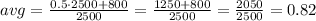
The average cost per ball is $0.82
Now we need to determine the profit, which is the subtraction between the total earnt by the cost. We have:

The total profit will be $4,200 if the balls are sold at $2.5