Solution:
Given a circle;
Where
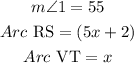
Applying the secant theorem for an interior case,
It states that the measure of an angle whose vertex lies in the interior of a circle is equal to half the sum of the angle measures of the arcs intercepted by it and its vertical angle.
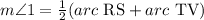
The equation becomes
![55\degree=[(1)/(2)((5x+2)+x)]\degree](https://img.qammunity.org/2023/formulas/mathematics/college/b3rqwpi27p0fy78cfh013kpdqmsqnopn2t.png)
Hence,
![55\operatorname{\degree}=(1)/(2)[(5x+2)+x]\degree]()
Solving for x
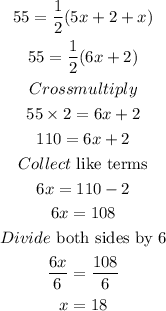
Hence, x is 18°
For arc RS
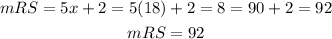
Hence, mRS is 92°