First, let's sketch the problem with the forces acting on the wheelchair:
1)
To calculate the acceleration, let's calculate the sum of forces in the surface direction:
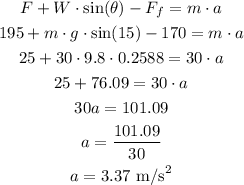
The acceleration is equal to 3.37 m/s².
2)
To find the normal force, let's calculate the sum of forces in the perpendicular direction to the table, and equate this sum to zero, since the wheelchair is not moving in this direction:
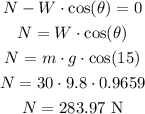
The normal force is equal to 283.97 N.