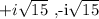
Step-by-step explanation
A root is a value for which a given function equals zero, so let's solve the equation
Step 1
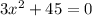
a) apply the subtraction property of equality and subtract 45 in both sides
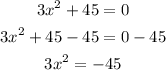
b)now, use the division property of equality to isolate square x,
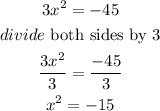
c) finally , take the square root in both sides
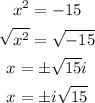
so, the answer is
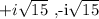
I hope this helps you