Question

A local zoo found that if the price of admission was $17, the attendance was about 1850 customers per week. When the price of admission was dropped to $13,attendance increased to about 2700 per week. Write a linear equation for the attendance in terms of the price,p. (A = mp+b)

Answer 1

It is given that the general equation is:

`A=mp+b`

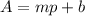
Here A is the number of people attending and p is the price of ticket.

Find the values of m and b by the conditions.

When A=1850, p=17 so it follows:

`1850=17m+b\ldots(i)`

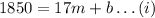
When A=2700, p=13 so it follows:

`2700=13m+b\ldots(ii)`

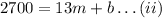
Subtract (ii) from (i) to get:

`\begin{gathered} 1850-2700=17m-13m \\ m=(1850-2700)/(4)=(-425)/(2)=-212.5 \end{gathered}`

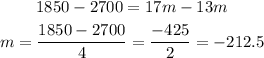
Substitute the value of m in (i) to get:

`\begin{gathered} 1850=17(-(425)/(2))+b \\ b=(10925)/(2)=5462.5 \end{gathered}`

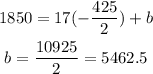
So the equation becomes:

`\begin{gathered} A=(-425)/(2)p+(10925)/(2) \\ 2A=-425p+10925 \end{gathered}`

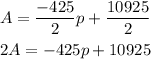
Hence the linear equation is 2A=-425p+10925.