Question

HelpWhat are the values ofA, B, and x?Ao=11xхOA = [?]°B = []BIVХB11

Answer 1

Since the given triangle is an isosceles triangle, we get:

`A=B\text{.}`

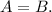
Now, we know that the interior angles of a triangle add up to 180 degrees, meaning:

`A+B+90^(\circ)=180^(\circ).`

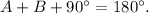
Substituting the first equation in the above equation, and solving for B we get:

`\begin{gathered} B+B+90^(\circ)=180^(\circ), \\ 2B=90^(\circ), \\ B=45^(\circ). \end{gathered}`

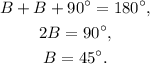
Substituting B=45° in the first equation we get:

`A=45^(\circ).`

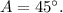
Finally, to find x we use the Pythagorean theorem:

`11^2+11^2=x^2\text{.}`

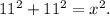
Solving the above equation we get:

`\begin{gathered} x^2=2\cdot11^2, \\ x=\sqrt[]{2\cdot11^2}, \\ x=11\sqrt[]{2}. \end{gathered}`

Answer:

`\begin{gathered} A=45^(\circ), \\ B=45^(\circ), \\ x=11\sqrt[]{2}. \end{gathered}`