Question

Sally can paint the office by herself in 10 hours. Dave can do the same job in 7 hours. How long will it take if they do it working together? Answer in fraction.

Answer 1

The answer is 70/17 hours.

Given:

The time required by Sally to paint is, S = 10 hours.

The time required byDave to paint is, D = 7 hours.

The objective is to find the number of hours it will take if they do it working together.

Work done by Sally in 1 hour can be calculated as,

`\begin{gathered} 10\text{ hours = 1 work} \\ 1\text{ hour=}(1)/(10)work \end{gathered}`

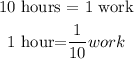
Work done by Dave in 1 hour can be calculated as,

`\begin{gathered} 7\text{ hours=1 work} \\ 1\text{ hour=}(1)/(7)work \end{gathered}`

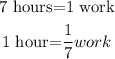
The work completed by both together in 1 hour can be calculated as,

`\begin{gathered} W(1)=(1)/(10)+(1)/(7) \\ =(7+10)/(7\cdot10) \\ =(17)/(70) \end{gathered}`

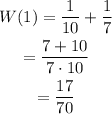
Now, the time required to complete the work together can be calculated as,

`\begin{gathered} T=(1)/(W(1)) \\ =(1)/((17)/(70)) \\ =(70)/(17) \end{gathered}`

Hence, the time required to complete the work together is 70/17 hours.