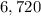Question

Evaluate the following expression.P(8,5)

Answer 1

We will investigate how to evaluate the permutations.

A permutation is a special function that is used for counting principle. It allows for counting objects in a space of ( n ) with ( r ) number of objects to be re-arranged in that space with significance given to the order in which the objects are arranged.

The general notation used to evaluate permutations is as such:

`^nP_r\text{ OR P ( n , r )}`

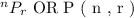
The special function of permutations ( P ) is approximated by the factorial composition as follows:

`^nP_r\text{ OR P ( n , r ) = }(n!)/((n-r)!)`

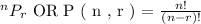
We will use the above notation and relation to determine the number of ways 5 objects can be arranged regardless of order in a space of 8.

`\begin{gathered} P\text{ ( 8 , 5 ) = }\frac{8!}{(8\text{ - 5 )!}} \\ \\ P\text{ ( 8 , 5 ) = }\frac{8!}{(3\text{)!}} \\ \\ P\text{ ( 8 , 5 ) = }(8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1)/(3\cdot2\cdot1) \\ \\ P\text{ ( 8 , 5 ) = }8\cdot7\cdot6\cdot5\cdot4 \\ \\ P\text{ ( 8 , 5 ) = }6,720 \end{gathered}`

Therefore, the solution to the expression is:

`6,720`