Question

A store did $54,000 in sales in 2017, and $67,000 in 2018.(a) Assuming the store's sales are growing linearly, find the growth rate d.(b) Write a linear model of the form Pt=P0+dt to describe this store's sales from 2017 onward.Pt= (c) Predict the store's sales in 2025.$ (d) When do you expect the store's sales to exceed $105,000? Give your answer as a calendar year (ex: 2020).During the year

Answer 1

Given:

A store did $54,000 in sales in 2017, and $67,000 in 2018.

a)

To find the growth rate:

Since, the store's sales are growing linearly

We can use the formula,

`\begin{gathered} d=(y_2-y_1)/(x_2-x_1) \\ =(67,000-54,000)/(2018-2017) \\ =13,000 \end{gathered}`

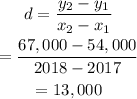
Hence, the growth rate d is 13,000.

b)

To write a linear model of the form Pt=P0+dt to describe this store's sales from 2017 onwards:

So, the linear equation is

`P_t=54,000+13,000t`

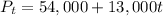
c) To predict the store's sales in 2025.

The total number of year from 2017 to 2025 is 8.

Let us substitute t=8 in the above equation we get,

`\begin{gathered} P_t=54,000+13,000t \\ P_8=54,000+13,000(8) \\ =54,000+1,04,000 \\ =1,58,000 \end{gathered}`

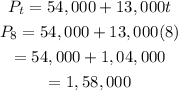
Therefore, the store's sales in 2025 is $ 1,58,000.

d) To find the year at which the sales is exceed $1,05,000

Then the linear equation becomes,

`\begin{gathered} 1,05,000=54,000+13,000t \\ 13,000t=1,05,000-54,000 \\ 13,000t=51,000 \\ t=3.923 \end{gathered}`

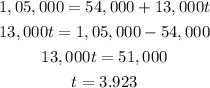
Therefore, 2017+3.9 Years

We will get, the sales will get exceed in the 2020 itself.

Hence, the sales will get exceed $1,05,000 in the year 2020.