What is the answer ? A. B. C. or D?

Question

asked Dec 27, 2023 185k views

1 Answer

Tino · Answer 1 · 2024-01-02T23:48:52+0000

By definition, a Right triangle is a triangle that has an angle that measures 90 degrees (which also called "Right angle").

For this case, you can identify that the triangle given in the exercise is a Right triangle.

To find the measure of the missing angle, you need to use Arccosine function, which is the inverse of the cosine function:

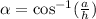
$\alpha=\cos ^(-1)((a)/(h))$

Where "α (alpha)" is the angle you must find, "a" is the adjacent side and "h" is the hypotenuse.

You can set up that, for this case:

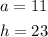
$\begin{gathered} a=11 \\ h=23 \end{gathered}$

Then, substituting values and evaluating, you get that the measure of the angle is:

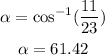
$\begin{gathered} \alpha=\cos ^(-1)((11)/(23)) \\ \alpha=61.42\degree \end{gathered}$

Rounding the answer to nearest whole degree, you get:

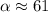
$\alpha\approx61\degree$

The answer is: Option C.