Question

write an explicit formula for the sequence determined by the recursion formula: f(1) = 5; f(n) = 2f(n-1)

Answer 1

Let's find the initial terms of the sequence:

f(1) = 5

f(2) = 2*5 = 10

f(3) = 2*10 = 20

f(4) = 2*20 = 40

So, the ratio of the sequence is 2 = 40/20 = 20/10

And the general explicit formula is:

`\begin{gathered} f_n=f_1\cdot r^(n-1) \\ \end{gathered}`

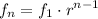
Substituting the values, we have the explicit formula for this sequence:

`f_n=5\cdot2^(n-1)_{}`

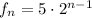
f(1) means the first term of the sequence;

f(2) means the second term of the sequence;

f(n) is a general formula for the "n" term

So, f(n) = 2f(n-1) is a formula to find the term "n" using the term "n-1" (the antecessor).

Here, we have an example:

f(1) = 5

f(n) = 2f(n-1)

If n = 2

f(2) = 2*f(2-1)

f(2) = 2*f(1)

f(2) = 2*5

f(2) = 10

If n=3

f(3) = 2*f(3-1)

f(3) = 2*f(2)

f(3) = 2*10

f(3) = 20