Question

Solve the following series. Remember to use your formulas and indicate your final answer. Find the sum of the first 20 terms of: 4, 7, 10, 13, ...

Answer 1

S₂₀ = 650

Explanation:

there is a common difference between consecutive terms in the series, that is

7 - 4 = 10 - 7 = 13 - 10 = 3

this indicates the series is arithmetic with sum to n terms

`S_(n)`
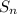
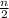`(n)/(2)` [ 2a₁ + (n - 1)d ]

where a₁ is the first term and d the common difference

here a₁ = 4 and d = 3 , then

S₂₀ =
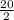`(20)/(2)` [ (2 × 4) + (19 × 3) ]

= 10(8 + 57)

= 10 × 65

= 650

Answer 2

From the terms of the sequence we are given, we can deduce that the next term of the sequence will be the previous one plus 3. Knowing this, the series we must consider is:

`\sum ^(19)_(n\mathop=0)4+3(n)`

And adding all the terms together we get

`\sum ^(19)_(n\mathop=0)4+3(n)=650`