We have a principal which compound its interest quarterly.
The annual nominal rate is 3.56%.
The principal is $1350.
We can express the amount in the account with the expression:
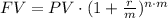
where FV: future value, PV: present value, r: annual interest rate, n: number of years, m: number of subperiods a year.
In this problem, r=0.0356, PV=1350 and m=12/3=4
In this case, for a period of 6 months, we have n=0.5, so the calculation gives a final vlaue of:
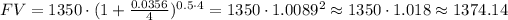
Substracting the principal of 1350, the interest is:
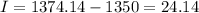
For a one-year period, n=1, so we can calculate the final value as:
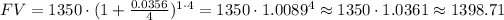
Again, by substracting the principal, we can get the compounded interest:

A. For a period of 6 months, the interest is $24.14.
B. The balance at 6 months from the deposit is $1374.14.
C. For a period of one-year, the interest is $48.71.
D. The balance at one year from the deposit is $1398.71.