Question

T and radius, then grapher nts a circle with a real now uxo on. Ty cus and a the locus the dire SAU b) 3x + 3y - 11x=-91 & x² + y² - Ax = 0 3 x² + y² - 2x By h • 4x + 4y² 1) x² + y² - Ty=0 ) x + y - 2ax +2byc 16x + 2y = 21 chvara d) 36x + 36y? - 36x +48y = -16 gurer Ha h (5, 3) and is concentric with x? par and concentric with the circles? + twice as far from (6,0) as from (0,0). such that the square of the distance points: (0,0), (6,0),(0,-4), and (5,1 -y=27 + 2y = -2 and tangent to the line 5x ent to the circle x² + y2 + 6x + 4y = (b) X = 2

Answer 1

b)

`3x^2+3y^2-11x=-91`

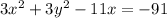
We will arrange the terms first

`3x^2-11x+3y^2=-91`

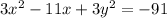
First, we will divide all the terms by 3 to make the coefficients of x^2 and y^2 equal to 1

`\begin{gathered} (3x^2)/(3)-(11)/(3)x+(3y^2)/(3)=-(91)/(3) \\ x^2-(11)/(3)x+y^2=-(91)/(3) \end{gathered}`

Now, divide the term of x by 2 to find the 2nd term of completing the square

`\because-((11)/(3))/(2)x=-(11)/(6)x`

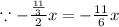
The first term is x and the 2nd term is -11/6

`\because(-(11)/(6))^2=(121)/(36)`

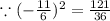
Then we must add and subtract 121/36

`\therefore x^2-(11)/(3)x+(121)/(36)-(121)/(36)+y^2=-(91)/(3)`

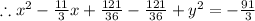
Now I will take the first 3 terms and make the bracket power 2 of them

`\because(x^2-(11)/(3)x+(121)/(36))=(x-(11)/(6))^2`
`\therefore(x-(11)/(6))^2-(121)/(36)+y^2=-(91)/(3)`

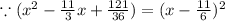
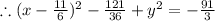
Add both sides by 121/36

`(x-(11)/(6))^2+y^2=-(971)/(36)`

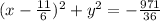
From this form r ^2 is a negative value then it could not be a real non zero

The equation does not represent a circle with a real non-zero radius