Question

A relation is plotted as a linear function on the coordinate plane starting at point A (0,3) and ending at point B (2, 7).What is the rate of change for the linear function and what is its initial value?Select from the drop-down menus to correctly complete the statements.The rate of change is 0 and 2 and 4 and 7 and the initial value is 0 and 2 and 3 and 7

Answer 1

Give the points, we can calcualte the slope, that is, the rate of change, using the following:

`m=(y_2-y_1)/(x_2-x_1)`

So, using points (0, 3) and (2, 7), we have:

`m=(7-3)/(2-0)=(4)/(2)=2`

Now, the slope-intercept form for linear graph is:

`y=mx+b`

Where we have m and b is the y-intercept, that is, the value of the function when x = 0, so the initial value.

Using the first point, (0, 3), we have:

`\begin{gathered} y=2x+b \\ 3=2\cdot0+b \\ 3=b \\ b=3 \end{gathered}`

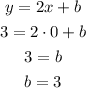
So, the inital value is 3.

That means that The rate of change is 2 and the initial value is 3.