To make things easier, we first write both quantities with scientific notation:
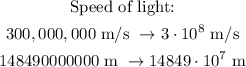
Now we can find how many seconds will it take the light to reach the sun with a simple division:
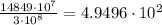
Therefore, it will take the light 4.9496x10^2 seconds to reach the sun.
Finally, to convert it to hours and days, we just have to divide by the corresponding equivalence:

Therefore, it will take the light 13.748x10^(-2) hours or 57.28x10^(-4) days to reach the sun.