Question

Plssss I need quick answers with tips I can understand

Answer 1

In a right traiangles, note that the longest side or the side facing the 90degrees is the hypotenuse.

Also, the side facing a given angle is the opposite

Then, the last side is adjacent.

Also, note the pythagorean theorem that;

`\begin{gathered} h^2=o^2+a^2 \\ o^2=h^2-a^2 \\ a^2=h^2-o^2 \\ \text{Where h= hypotenuse} \\ a=\text{ adjacent} \\ o=\text{opposite} \end{gathered}`

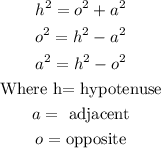
Also note the concept below;

`\begin{gathered} \text{SOH, CAH and TOA} \\ \text{Where SOH means }\sin \theta=(opposite)/(hypotenuse) \\ \text{CAH means }\cos \theta=(adjacent)/(hypotenuse) \\ \text{TOA means }\tan \theta=\frac{opposite}{\text{adjacent}} \end{gathered}`

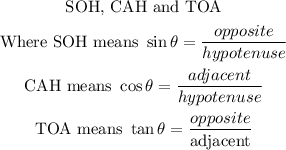
As explained y represents the hypotenuse because it is the longest side,

x represents the opposite side because it faces the given angle,

so 13 is the adjacent.

First, using TOA concept to get x;

`\begin{gathered} \text{Tan}\theta=(o)/(a) \\ \tan 45=(x)/(13) \\ x=13\tan 45 \\ x=13 \end{gathered}`

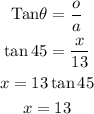
On getting x=13, the pythagoream theorem can be used to get the third side called the hypotenuse.

`\begin{gathered} h^2=o^2+a^2 \\ y^2=13^2+13^2 \\ y^2=169+169 \\ y^2=338 \\ y=\sqrt[]{338} \\ y=18.4 \end{gathered}`